Институт нефтегазовой геологии и геофизики им. А.А. Трофимука СО РАН находится на переднем крае новой парадигмы численного моделирования. О мировых тенденциях в этой сфере, о ведущихся в Институте работах и об их значении для науки и добывающей отрасли рассказал заведующий лабораторией математического моделирования многофизичных процессов в нативных и искусственных многомасштабных гетерогенных средах ИНГГ СО РАН к.ф.-м.н. Сергей Игоревич Марков.
– Сергей Игоревич, сегодня во всём мире уделяется большое внимание разработке алгоритмического и программного обеспечения, связанного с суперкомпьютерными технологиями. Чем это обусловлено?
– В первую очередь, необходимостью решать широкий спектр прикладных задач высокого разрешения. Вычислительные возможности сейчас очень широкие: в 2022-м году суперкомпьютеры уже достигли эксафлопсового уровня производительности. Один эксафлопс равен одному квинтиллиону операций с плавающей точкой в секунду. Работающему со скоростью одно вычисление в секунду человеку потребовалось бы примерно 32 миллиарда лет, чтобы сделать то, что машина может выполнить за секунду.
Если говорить о геофизических приложениях, то здесь к задачам большого разрешения относятся анализ разведочных данных, построение многомасштабных цифровых моделей месторождений и кернов. Математические методы (в частности, численное моделирование) представляют собой мощный аппарат для проведения таких научных исследований.
– Верно ли, что увеличение производительности компьютеров автоматически позволит быстрее получить качественный результат?
– Не совсем так. Специалисты суперкомпьютерных центров говорят о следующем парадоксе: машины сверхвысокой производительности уже существуют, но мало задач, использующих более сотни петафлопс на вариант. Это не означает, что нет формально поставленных задач – они есть. Однако существующие численные методы не всегда пригодны для их решения. Основная проблема связана с их устойчивостью и сложностью декомпозиции задачи на процессоры с целью разделить вычисления на независимые части, которые могут быть выполнены параллельно. Для эффективной работы суперкомпьютера нужны новые численные методы.
– Какими свойствами они должны обладать?
– Новые методы должны позволять учитывать как геометрическую, так и функциональную многомасштабности, которые возникают при решении геофизических задач. Сюда относятся новые методы декомпозиции области в контексте распределения задач по узлам вычислительных систем, а также методы визуализации. Об активной фазе решения указанной проблемы свидетельствует многообразие предлагаемых методов дискретизации математических моделей, симбиоз алгоритмов на базе искусственных нейронных сетей и численного моделирования.
Замечу, что в начале 1950-х годов подобная ситуация уже возникала. Тогда были заложены основы прикладной математики и программирования, которые способствовали развитию теории конечных разностей, методов Монте-Карло, быстрого преобразования Фурье. Сегодня мы являемся свидетелями аналогичного этапа становления прорывных технологий.
– Чем в этой связи занимаются в лаборатории математического моделирования многофизичных процессов в нативных и искусственных многомасштабных гетерогенных средах ИНГГ СО РАН?
– Мы ведём исследования с применением современных вычислительных схем методов конечных элементов и машинного обучения для численного решения широкого круга прикладных задач геофизики. Это изучение свойств образцов осадочных пород при использовании цифрового керна, анализ влияния процессов переноса при бурении скважин на электромагнитные свойства околоскважинного пространства, идентификация рудных месторождений по результатам электромагнитных измерений, волновые процессы в гетерогенных средах.
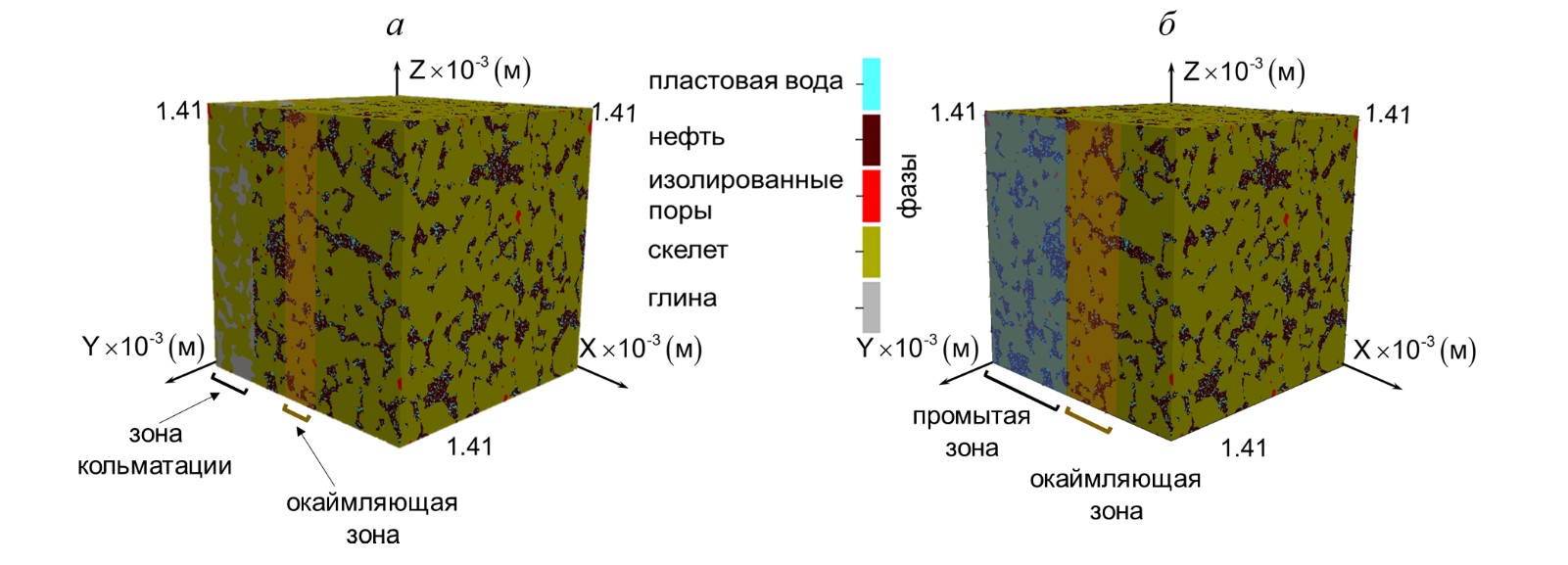
Пример решаемой в ИНГГ СО РАН задачи об инжекции бурового раствора в пористый нефтеводонасыщенный образец песчаника
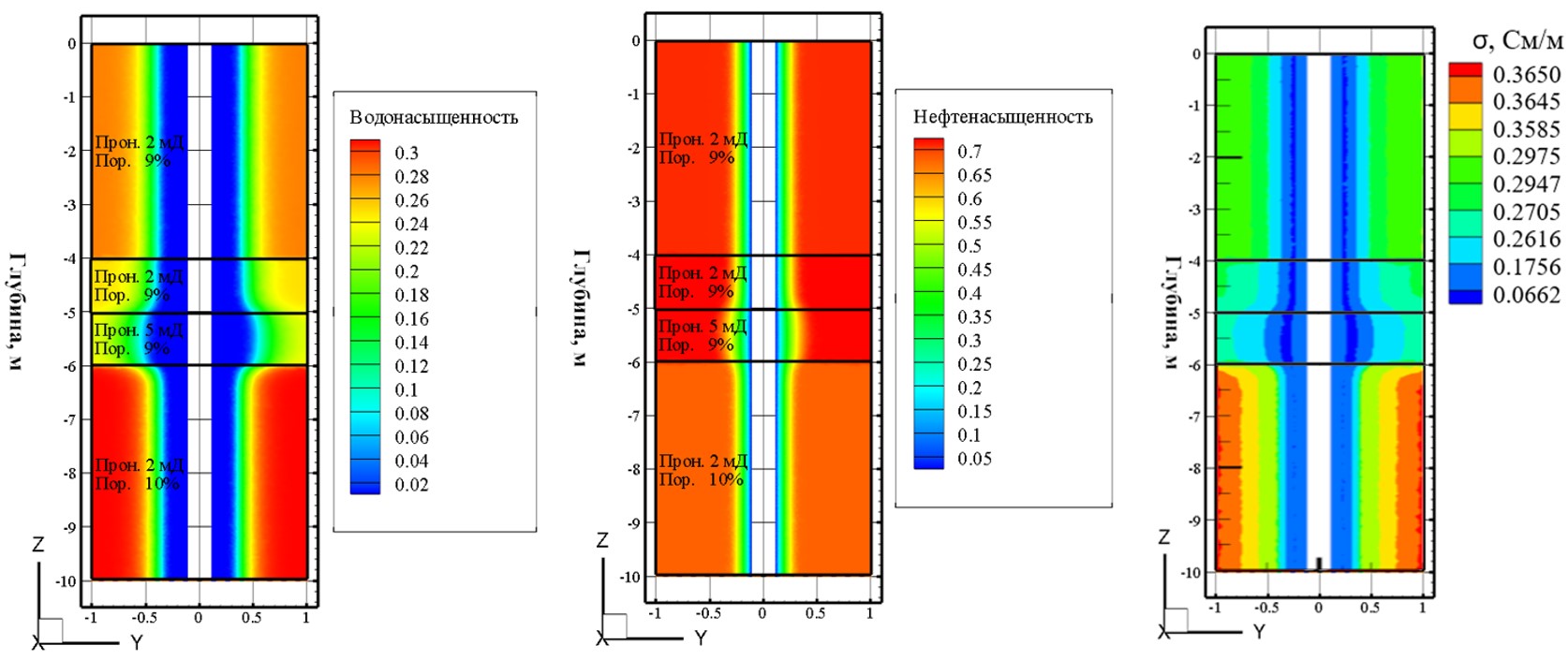
Влияние процессов переноса на электрические свойства околоскважинного пространства – задача, также решённая в ИНГГ СО РАН
Указанные задачи характеризуются не только высоким контрастом физических свойств изучаемых объектов, но и многомасштабностью как по пространству, так и во временной области. Обойти эти сложности позволяют неконформные и виртуальные методы конечных элементов.
– В чём их преимущества?
– Данные методы имеют большой практический потенциал, поскольку позволяют полностью отказаться от классической идеи базисной системы конечно-элементных схем и работать с функциональным пространством посредством проекторов. Это позволяет существенно сократить размер дискретного аналога задачи и снизить затраты вычислительных ресурсов, связанных с пространственной дискретизацией. Естественный параллелизм алгоритмов достигается за счёт применения иерархических сеточных моделей и первичной кластеризации структурных особенностей расчётных областей.
– Какое будущее у развиваемых в лаборатории разработок?
– Проводимые нами исследования были поддержаны Российским научным фондом. В рамках нового проекта мы предложим новые методы и эффективные алгоритмы решения прикладных задач разведочной геофизики в северных регионах России.
Хочу подчеркнуть, что современная наука не создаётся в изолированных условиях. Практически ценные результаты могут быть получены только в тесном сотрудничестве со специалистами в прикладных областях. В стенах Института мы взаимодействуем с коллективом лаборатории многомасштабной геофизики; с Никитой Александровичем Голиковым обсуждаем сценарии физических экспериментов. Главное в этом деле – формально поставить задачу и интерпретировать полученные результаты с точки зрения геофизики. Здесь нам очень помогает научный куратор нашей лаборатории – академик Михаил Иванович Эпов. Мы очень благодарны Михаилу Ивановичу за постановку новых прикладных задач и плодотворные обсуждения результатов.
Опубликовано пресс-службой ИНГГ СО РАН
Иллюстрации предоставлены С.И. Марковым